张力元的个人站

分享·技术·生活

MATLAB学习笔记第四篇：绘制图像

发表于 分类于

简介

本文针对MATLAB最常用的绘图方法进行简单的介绍。

1、采用plot()绘图

1
plot(cos(0:pi/20:2*pi))

绘图结果：

image-20201011111903246

1
plot(cos(0:pi/20:2*pi),'or')

绘图结果：

image-20201011113022305

1
plot(cos(0:pi/20:2*pi),'--r')

绘图结果：

image-20201011113137297

1
2
3
4
hold on
plot(cos(0:pi/20:2*pi),'or')
plot(sin(0:pi/20:2*pi),'--g')
hold off

绘图结果：

image-20201011142534019

在程序的开头和结尾添加hold on/hold off可以将程序中两个图线在一个界面上同时显示；若不添加，则只显示第二个（最新的）图线。

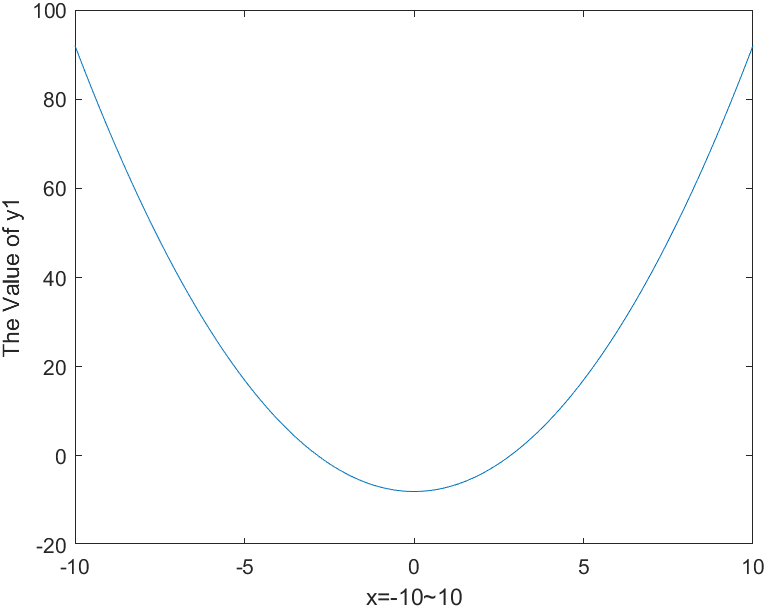
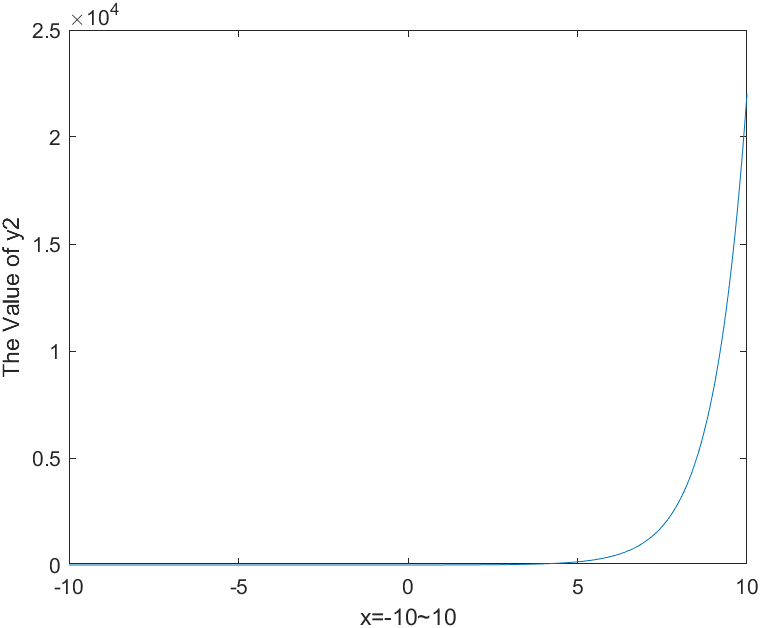
2、多图绘制

（1）分别在两个窗口显示

1
2
3
4
5
6
7
x=-10:0.01:10;
y1=x.^2-8;
y2=exp(x);
figure,plot(x,y1);
xlabel('x=-10~10')
ylabel('The Value of y1')
figure,plot(x,y2);

函数y1图线绘图结果：

image-20201011143839253

函数y2图线绘图结果：

image-20201011144011983

（2）在一个窗口显示

在matlab中，同一窗口显示多个图，使用subplot函数实现。

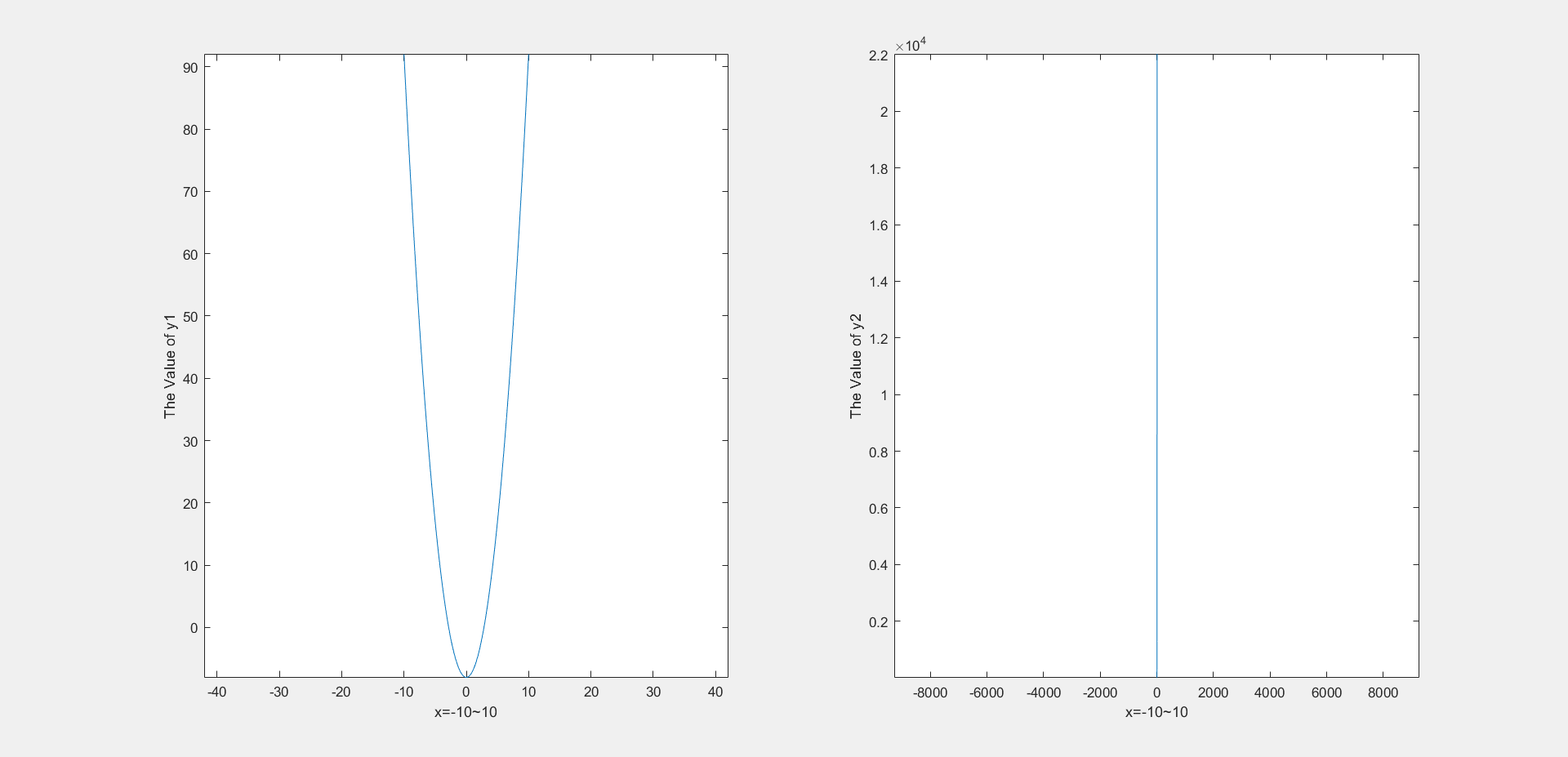
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
x=-10:0.01:10;
y1=x.^2-8;
y2=exp(x);

subplot(1,2,1);
plot(x,y1);
xlabel('x=-10~10')
ylabel('The Value of y1')
axis equal

subplot(1,2,2);
plot(x,y2);
xlabel('x=-10~10')
ylabel('The Value of y2')
axis equal

两个函数在同一个界面中显示：

image-20201011144640110

但是这里存在一个问题，我们可以发现第二个函数显示的是一条直线而不是分窗情况下的曲线，但是我们放大后可以发现图线和分窗情况的曲线是相同的。

这里涉及到坐标轴的设置和缩放问题，主要通过调整axis函数来进行视图上的调整，以下代码作为调整axis函数的展示：

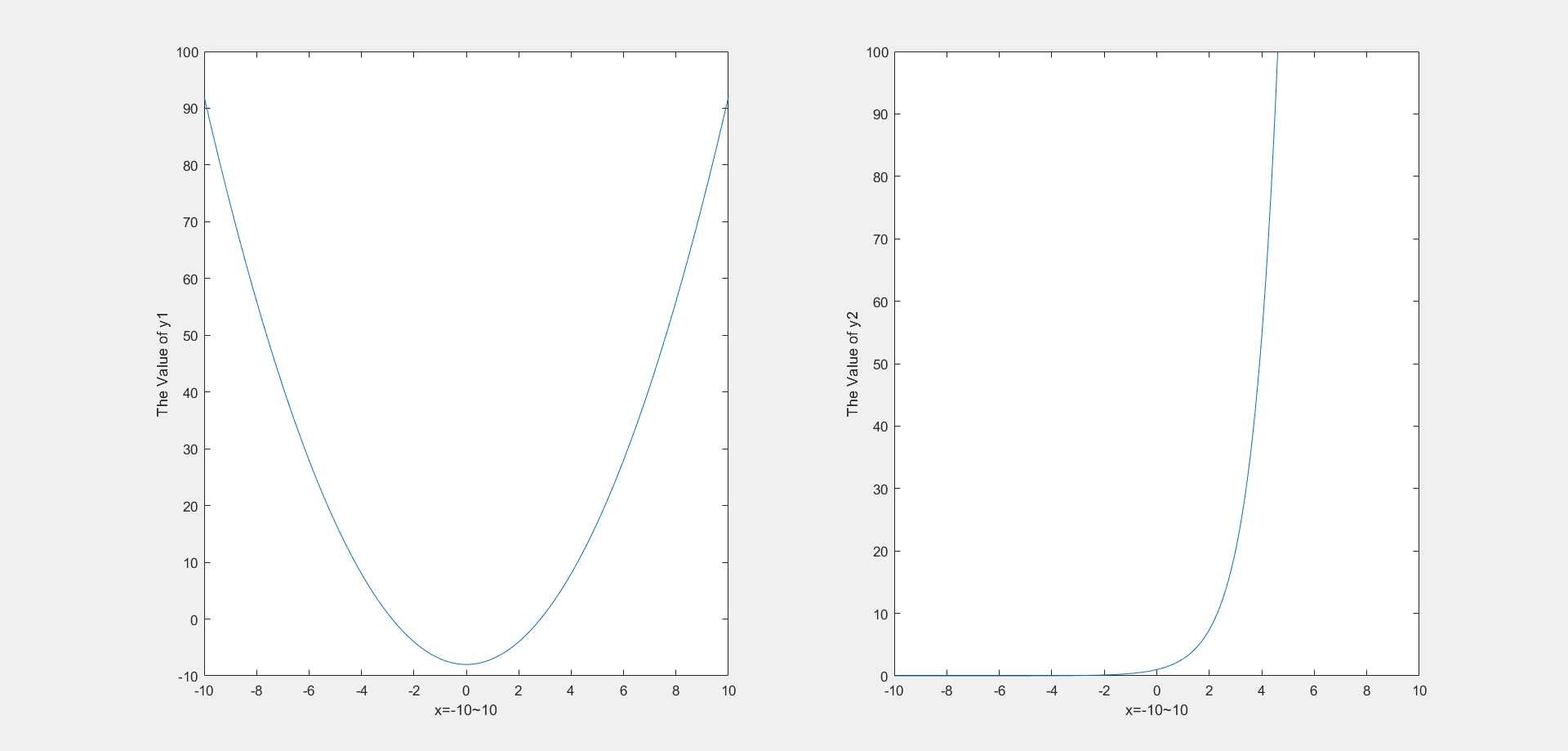
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
x=-10:0.01:10;
y1=x.^2-8;
y2=exp(x);

subplot(1,2,1);
plot(x,y1);
xlabel('x=-10~10')
ylabel('The Value of y1')
axis([-10 10 -10 100])

subplot(1,2,2);
plot(x,y2);
xlabel('x=-10~10')
ylabel('The Value of y2')
axis([-10 10 0 100])

调整坐标轴后的函数图像显示：

image-20201011145851455

在这里我们规定了横坐标轴的范围是（-10，10），纵坐标轴的范围有所不同，函数y1的纵坐标范围是（-10，100），函数y2的纵坐标轴范围是（0，100）。通过调整坐标轴我们可以更加直观的观察到函数的形状，为我们分析函数的分布提供了有效的方式。

其它关于axis函数的用法参考matlab官方文档。

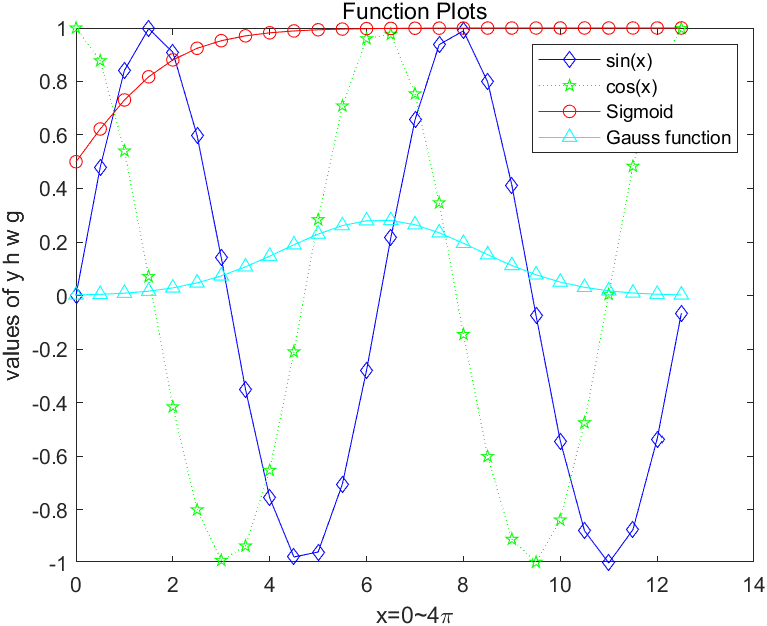
3、图例标签

1
2
3
4
5
6
7
8
9
10
x=0:0.5:4*pi;
y=sin(x);
h=cos(x);
w=1./(1+exp(-x));
g=(1/(2*pi*2)^0.5).*exp((-1.*(x-2*pi).^2./(2*2^2)));
plot(x,y,'bd-',x,h,'gp:',x,w,'ro-',x,g,'c^-');
xlabel('x=0~4\pi');
ylabel('values of y h w g');
title('Function Plots');
legend('sin(x)','cos(x)','Sigmoid','Gauss function ');

绘图结果：

image-20201011151225024

在这里我们设置了输入值x的范围是（0，4π），函数有四个，分别用不同的图线绘制，图中还标记了不同图线对应的图例。

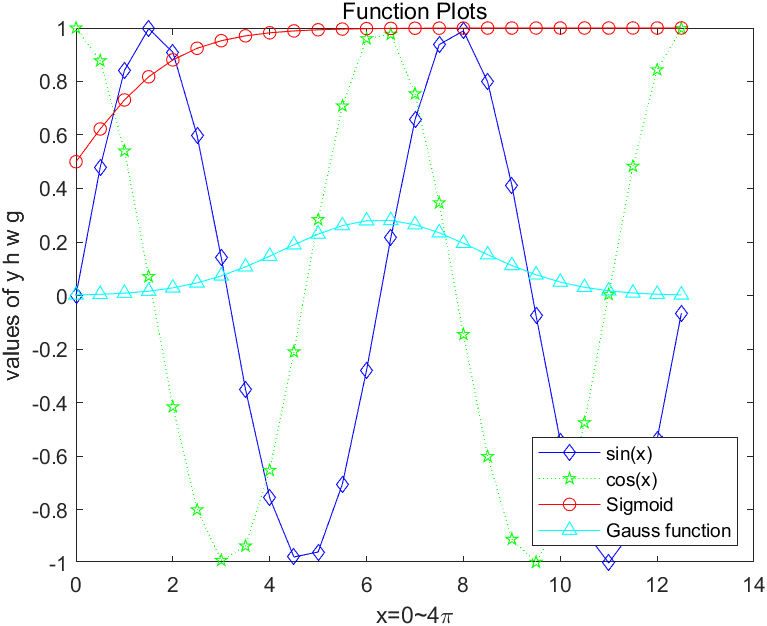
有时默认的图例位置不佳，我们可以调整图例的位置：

1
2
3
4
5
6
7
8
9
10
x=0:0.5:4*pi;
y=sin(x);
h=cos(x);
w=1./(1+exp(-x));
g=(1/(2*pi*2)^0.5).*exp((-1.*(x-2*pi).^2./(2*2^2)));
plot(x,y,'bd-',x,h,'gp:',x,w,'ro-',x,g,'c^-');
xlabel('x=0~4\pi');
ylabel('values of y h w g');
title('Function Plots');
legend('sin(x)','cos(x)','Sigmoid','Gauss function ','Location','southeast');

image-20201011152228353

可以看到图例的位置发生了改变，从右上角移动到了右下角。

常用的图例位置关键词：northeast 右上角，southeast 右下角，northwest 左上角，southwest 左下角。

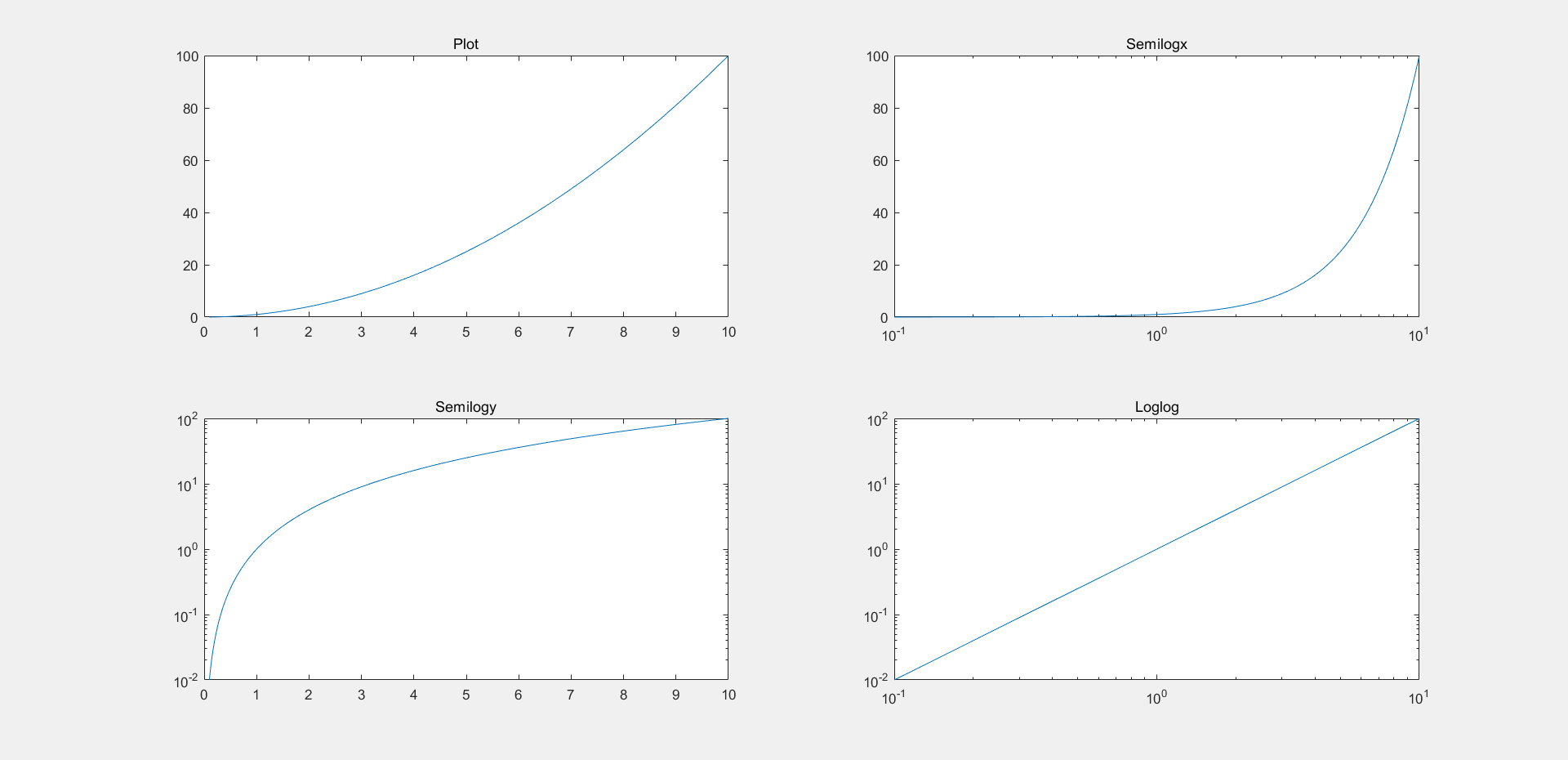
4、非线性绘图

图中的坐标轴通过一定的数学改变得到新的坐标图，例如对x轴或者y轴取对数后进行绘图。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
x=logspace(-1,1,100);
y=x.^2;
%线性绘图
subplot(2,2,1);
plot(x,y);
title('Plot');
%x轴采用log
subplot(2,2,2);
semilogx(x,y);
title('Semilogx');
%y轴采用log
subplot(2,2,3);
semilogy(x,y);%y轴采用log
title('Semilogy');
%两个轴都取对数
subplot(2,2,4);
loglog(x,y);
title('Loglog');

绘图结果：

image-20201011153151578

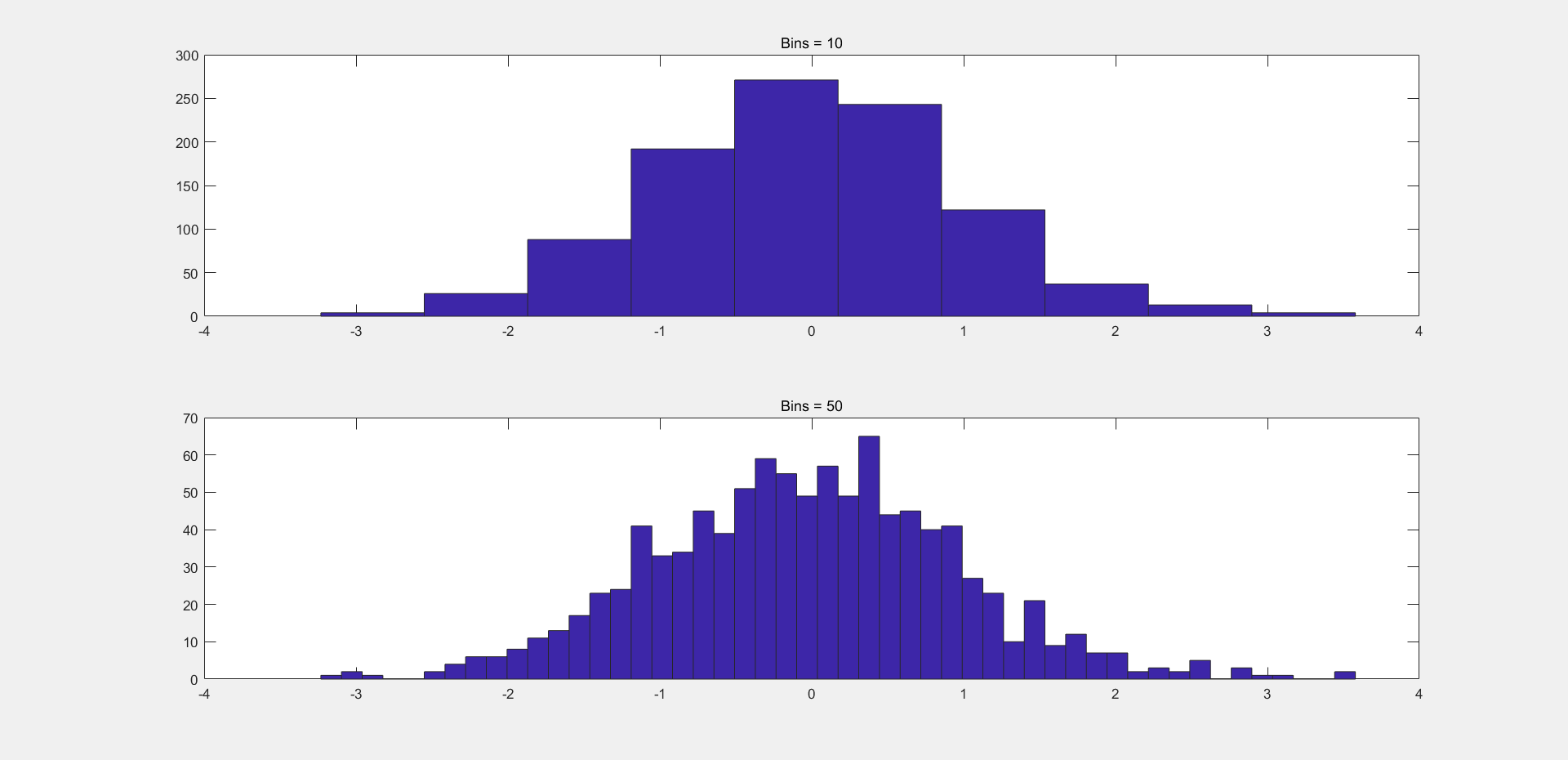
5、统计图的绘制

（1）直方图的绘制

直方图直观的反映了数据的一种分布方式，在工程中有着极为广泛的应用。例如在图像处理领域中，我们需要面对图像二值化的阈值选择问题，通过直方图进行一个灰度图的像素统计，我们可以直观的观察到合适的阈值点进行最优的灰度阈值分割；同样我们也可以通过直方图均衡化（Histogram Equalization）对图像进行均衡处理。

1
2
3
4
5
6
7
8
9
10
%y是在1~1000之间产生的随机数，通过对随机数进行统计得到直方图
y=randn(1,1000);

subplot(2,1,1);
hist(y,10);
title('Bins = 10');

subplot(2,1,2);
hist(y,50);
title('Bins = 50');

绘图结果：

image-20201011154721090

除了垂直于x轴分布的二维直方图，我们还可以绘制出垂直于y轴分布的二维直方图：

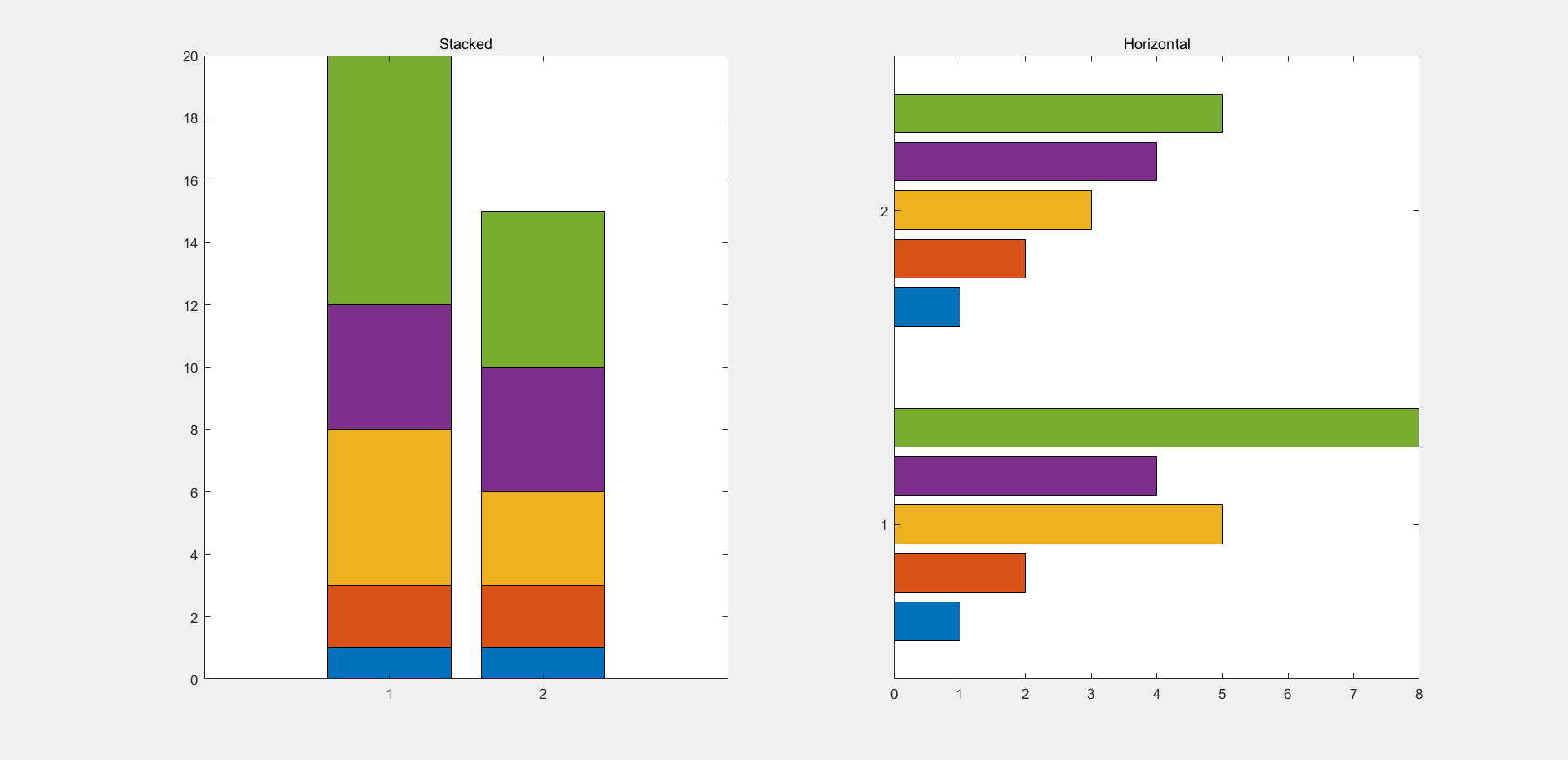
1
2
3
4
5
6
7
8
9
10
11
x=[1 2 5 4 8];
y=[x;1:5];

subplot(1,2,1);
% bar(y,'stacked');
bar(y,'stacked');
title('Stacked');

subplot(1,2,2);
barh(y);
title('Horizontal');

绘图结果：

image-20201011190753321

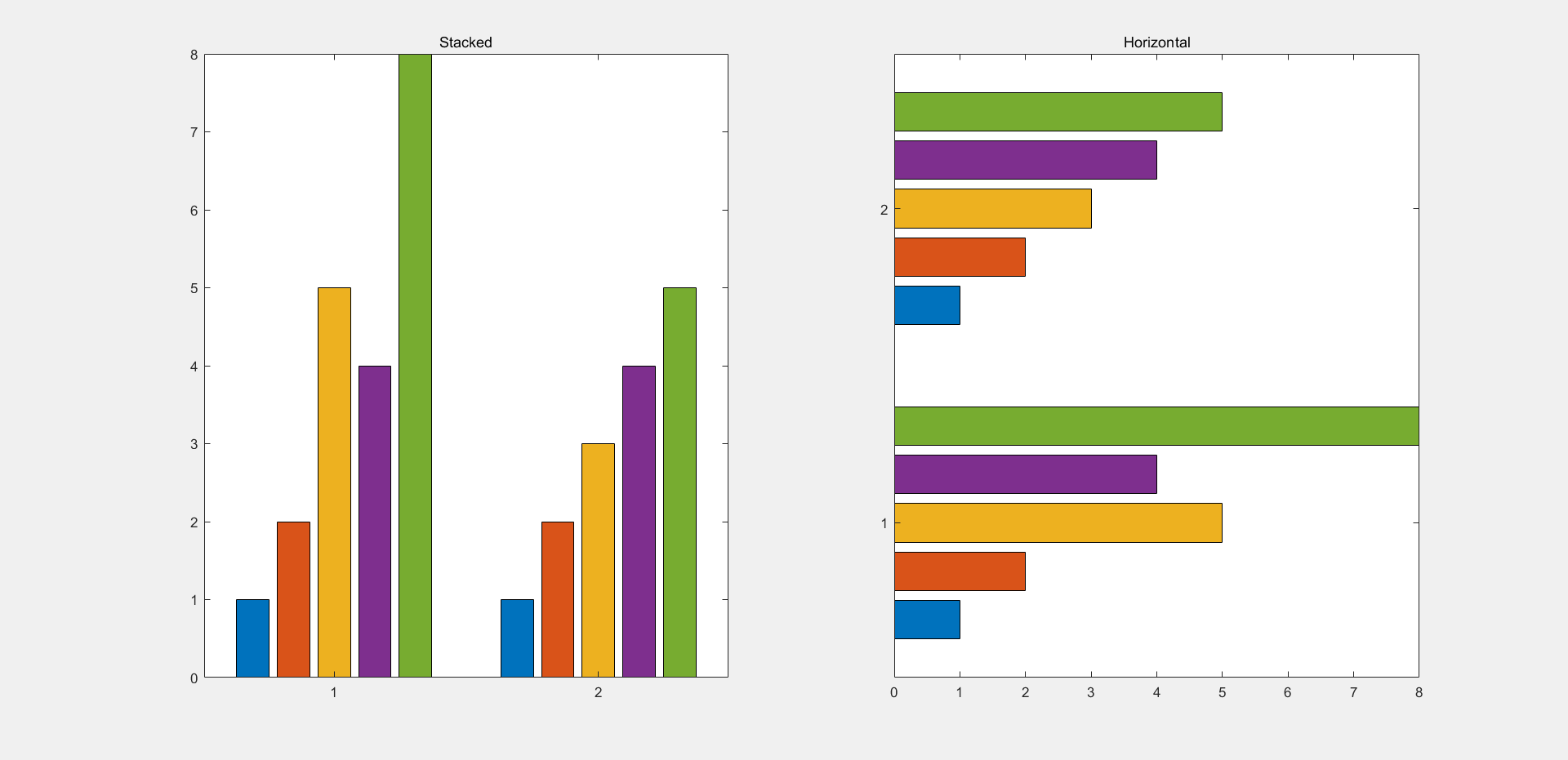
在本段程序中，语句bar(y,’stacked’)里还有一个参量’stacked’，在这里通过了这个参量实现了两行矩阵中元素占比在一个直方中显示，若去掉这个参量，结果如下图所示：

image-20201011191533699

（2）圆饼图的绘制

除了通过直方图进行数据的统计，我们还可以通过圆饼图对数据进行统计。

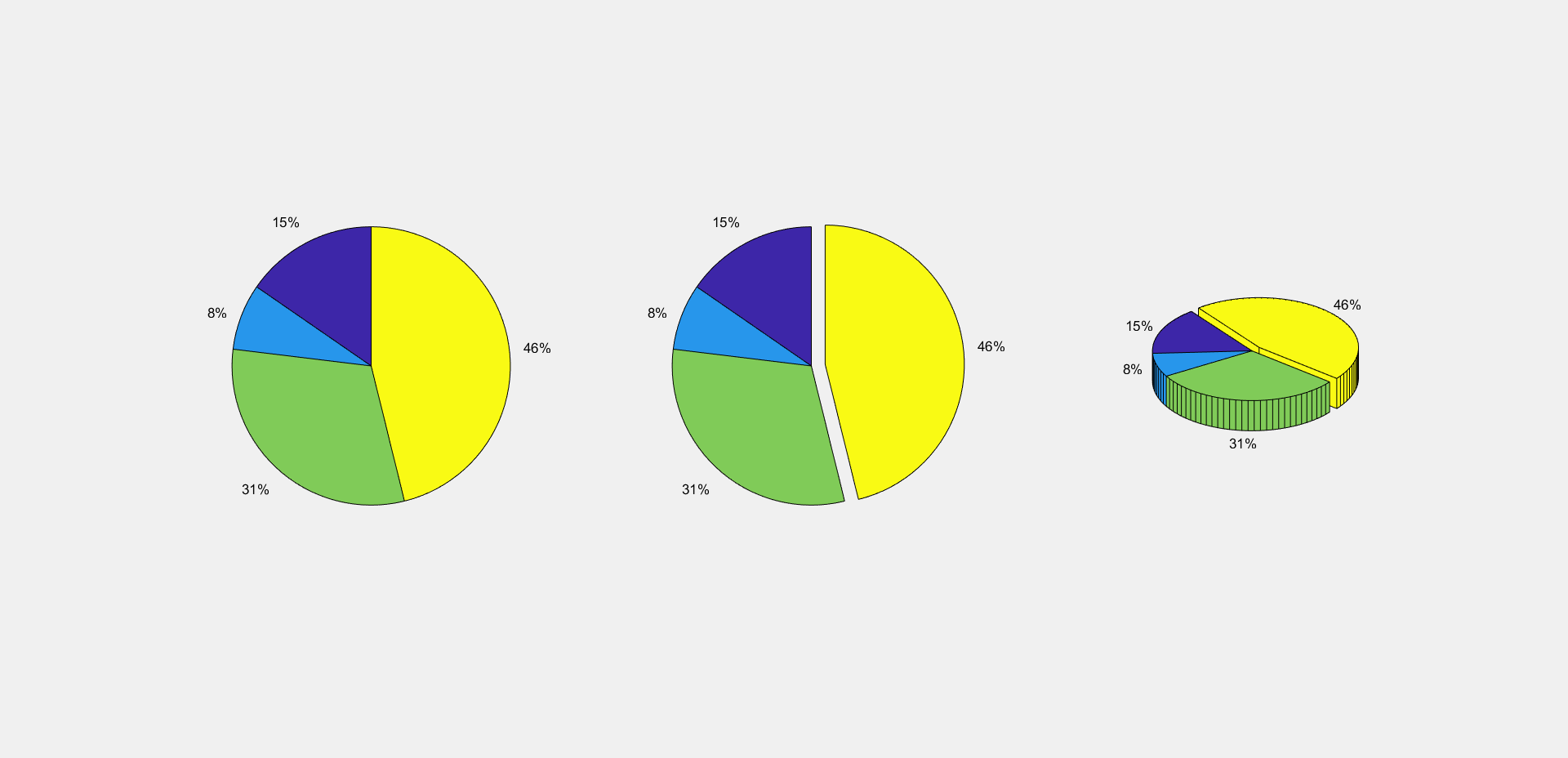
1
2
3
4
5
6
7
8
9
a=[10 5 20 30];
subplot(1,3,1);
pie(a);

subplot(1,3,2);
pie(a,[0,0,0,1]);

subplot(1,3,3);
pie3(a,[0,0,0,1]);

绘图结果：

image-20201011184107546

在这里我们要注意的是饼图的比例计算问题，饼图中比率的获得：X中的元素x[i]/sum(X)，也就是说单个元素的值/所有元素的值。若要将所有元素所占比例的色块区分开，可以设置pie函数中矩阵的参数。

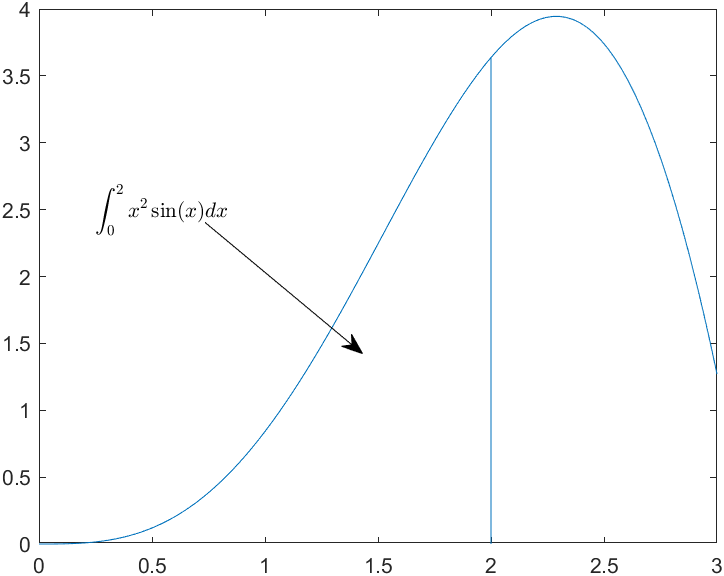
6、加入函数公式

1
2
3
4
5
6
7
x=linspace(0,3);
y=x.^2.*sin(x);
plot(x,y);
line([2,2], [0,2^2*sin(2)]);
str = '$$ \int_{0}^{2} x^2\sin(x) dx $$';%laTex公式表达式
text(0.25,2.5,str,'Interpreter','latex');%表示公式所在图中的位置
annotation('arrow', 'X', [0.32,0.5],'Y',[0.6,0.4]);%语句代表的是箭头的X和Y的位置

绘图结果：

image-20201011155521671

图中有一条直线，起点为（2，0），终点为（2，2^2*sin（2））。函数line的用法如下：

（1）line([起点横坐标，终点横坐标],[起点纵坐标，终点纵坐标]，’linestyle’，’线形’，’color’，’颜色’) 其中线形和颜色参考plot中的’-‘和’r’。

（2）line(A,B)中，A和B是相同大小的矩阵，会在对应的每一列做一条直线；同理在line(A,B,C)中，相应地会在三维空间中画一条线。在这里所说的A,B,C均是N*N的矩阵，得到的线条的数目就是矩阵的列数N列。

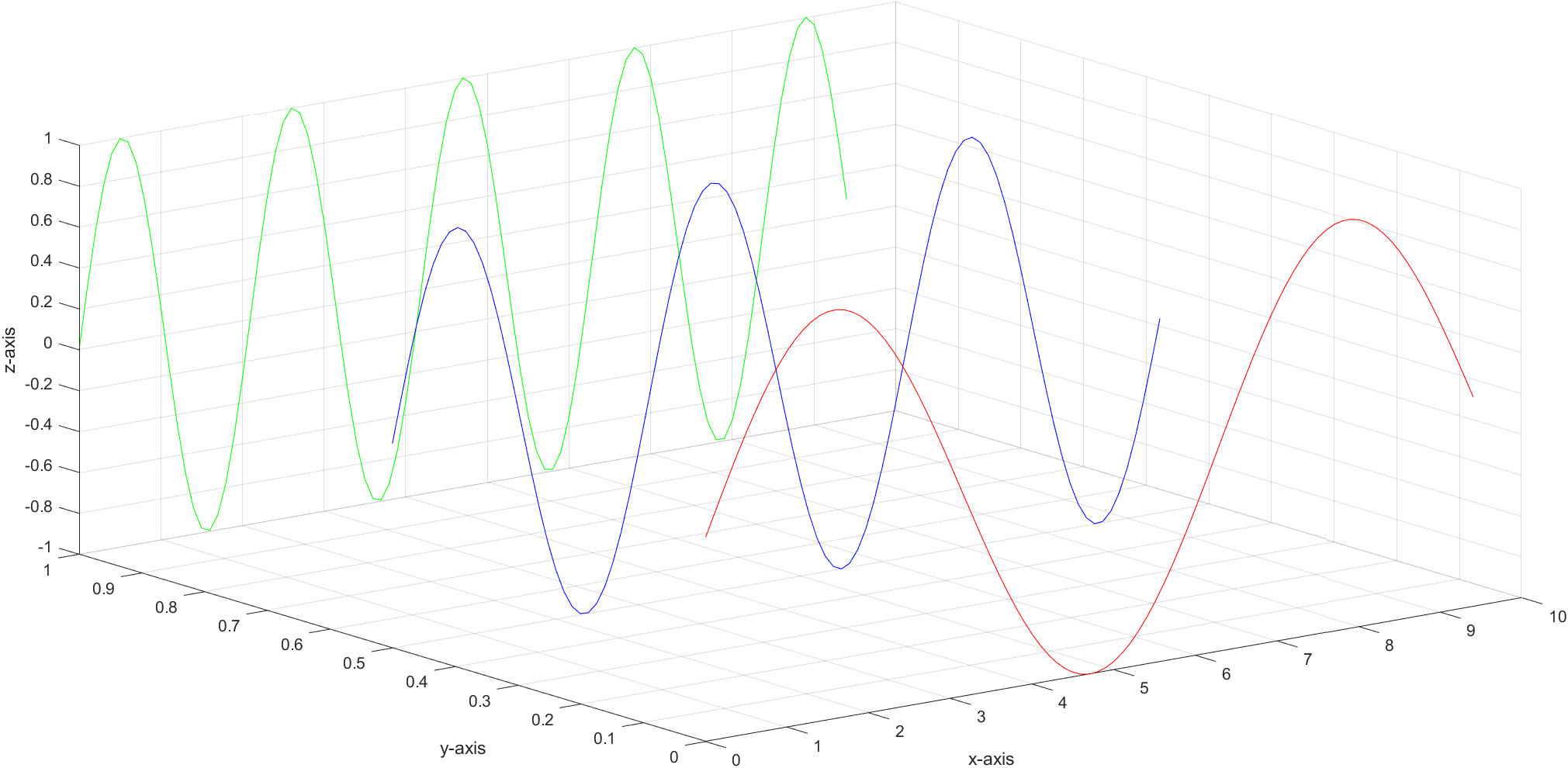
7、3D图

（1）简单的3D图绘制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
x=0:0.1:3*pi;
z1=sin(x);
z2=sin(2*x);
z3=sin(3*x);

y1=zeros(size(x));
y3=ones(size(x));
y2=y3./2;

plot3(x,y1,z1,'r',x,y2,z2,'b',x,y3,z3,'g');

grid on;
xlabel('x-axis');
ylabel('y-axis');
zlabel('z-axis');

绘图结果：

image-20201011164134388

本程序中，zeros函数和ones函数分别代表全一和全零的矩阵操作。在这里x是一个从0到2π的一个向量，而size（x）函数可以得到x这个向量的大小，之后通过zeros函数和ones函数可以将向量转化为一个标量数。另外，在本例程中，grid on表示图中显示网格，相同的grid off表示关闭网格的显示。

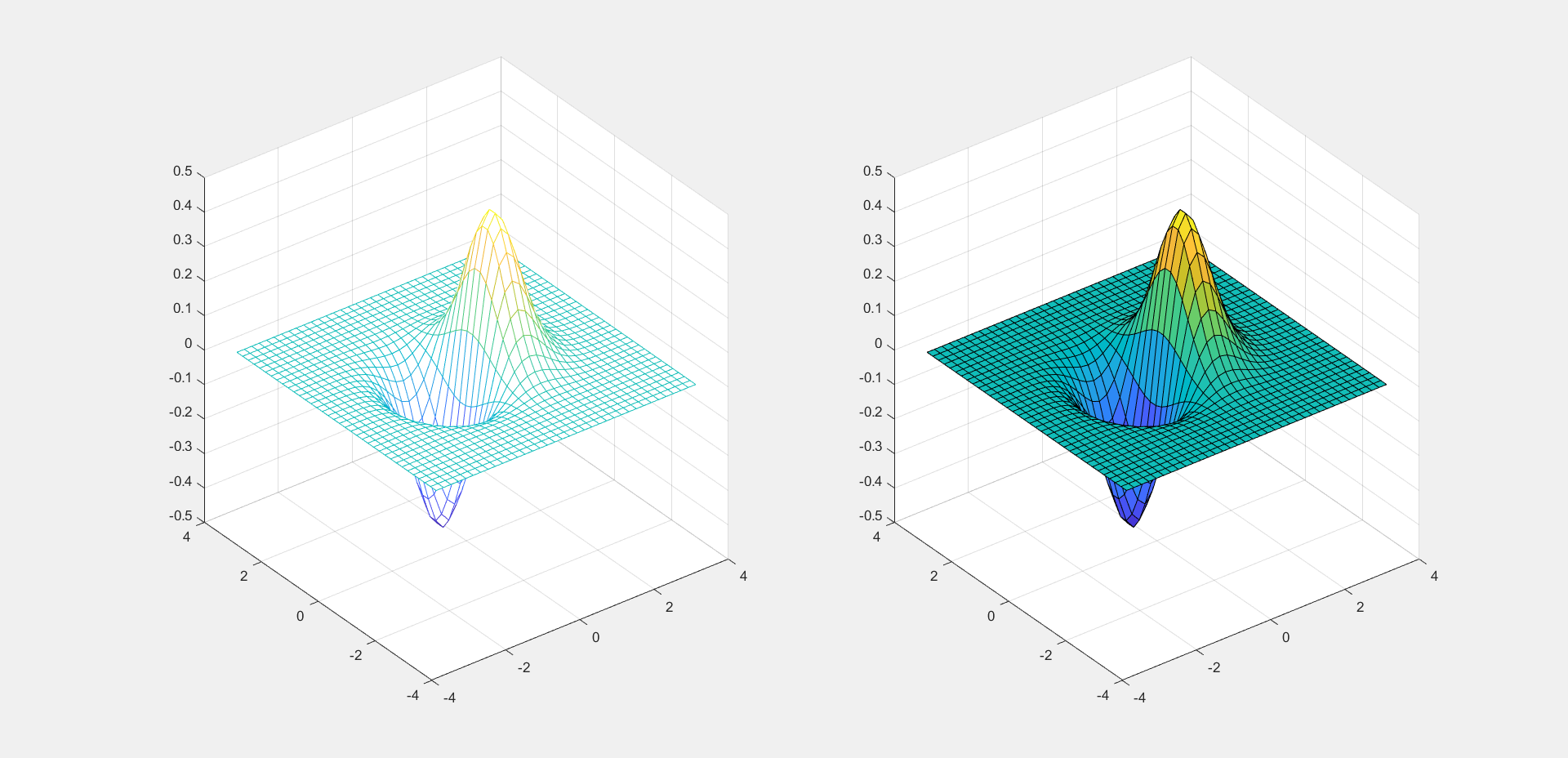
（2）3D图的绘制

1
2
3
4
5
6
7
8
x=-3.5:0.2:3.5;
y=-3.5:0.2:3.5;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
subplot(1,2,1);
mesh(X,Y,Z);
subplot(1,2,2);
surf(X,Y,Z);

绘图结果：

image-20201011165444039

本例程中[X,Y]通过meshgrid函数创建了一个矩阵，meshgrid函数的参数是矩阵的大小。Z是所要实现的函数，输入参数是一个二维向量。在这里使用了mesh函数和surf函数进行三维曲面的绘制，可以看到二者都可以绘制出函数的图像，但是二者又有所不同，mesh函数侧重于绘制出由彩色线条组成的三维网格图，而surf函数侧重于通过色彩描述三维图像的分布。

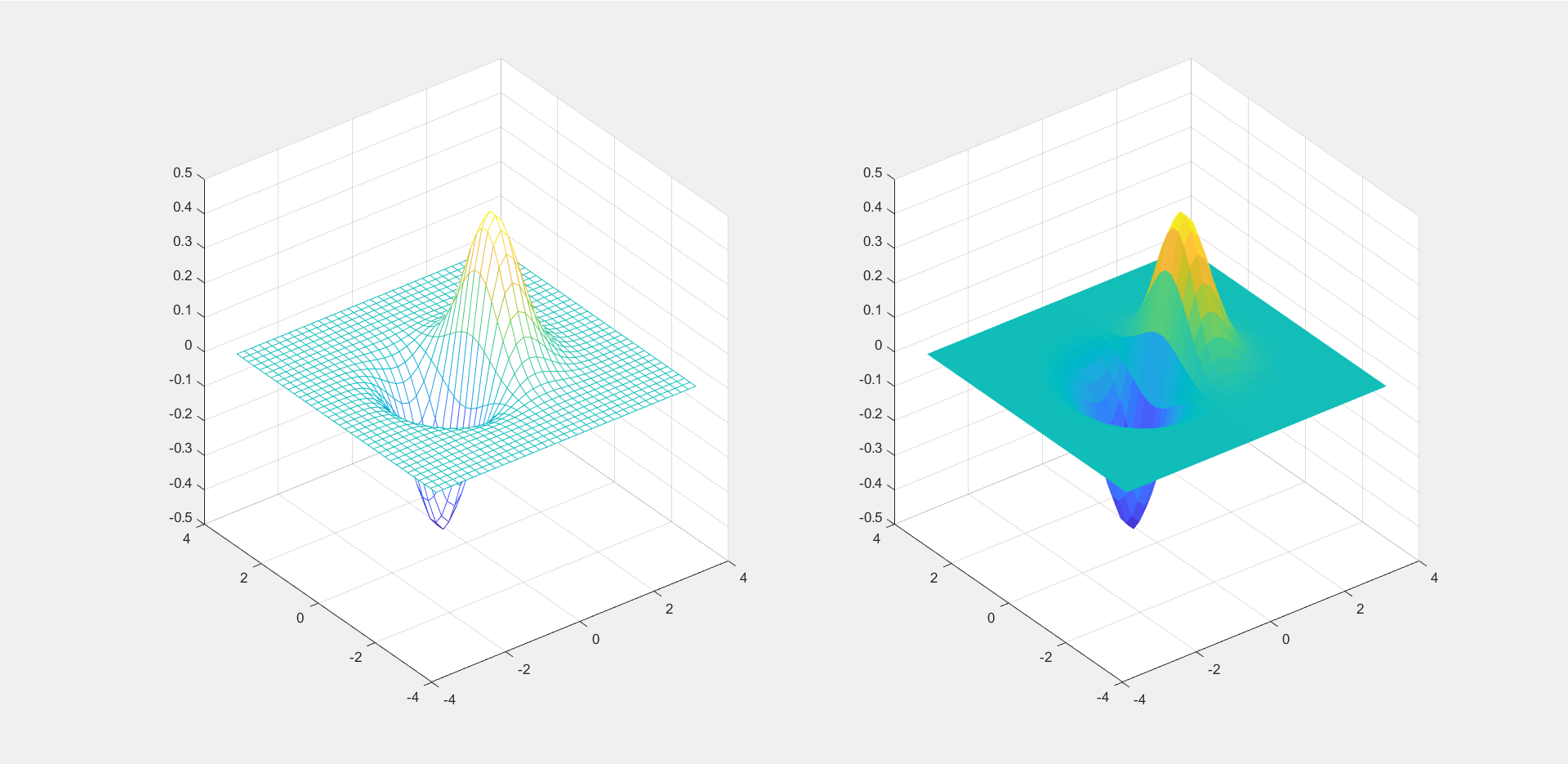
当执行以下代码时，我们可以发现有如下变化：

1
2
3
4
5
6
7
8
x=-3.5:0.2:3.5;
y=-3.5:0.2:3.5;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
subplot(1,2,1);
mesh(X,Y,Z);
subplot(1,2,2);
surf(X,Y,Z,'EdgeColor','none');

绘图结果：

image-20201011182657805

可以观察到，图中通过色彩变化描述了整体的幅度上的变化。

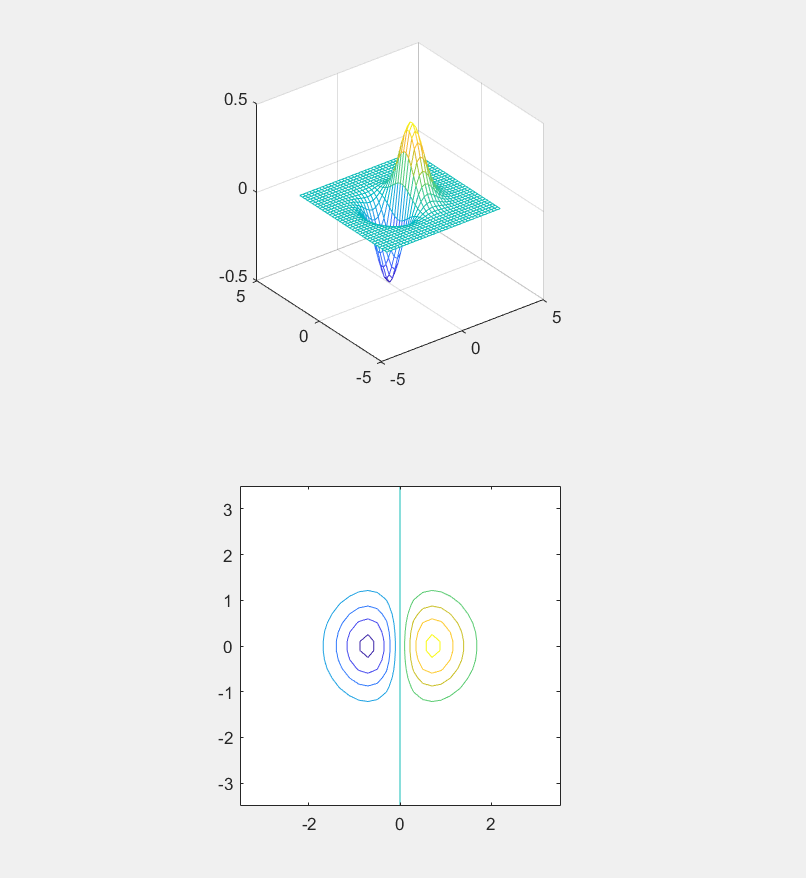
我们还可以使用contour函数观察三维图像的梯度变化：

1
2
3
4
5
6
7
8
9
10
x=-3.5:0.2:3.5;
y=-3.5:0.2:3.5;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
subplot(2,1,1);
mesh(X,Y,Z);
axis square;
subplot(2,1,2);
contour(X,Y,Z);
axis square;

绘图结果：

image-20201011183127075

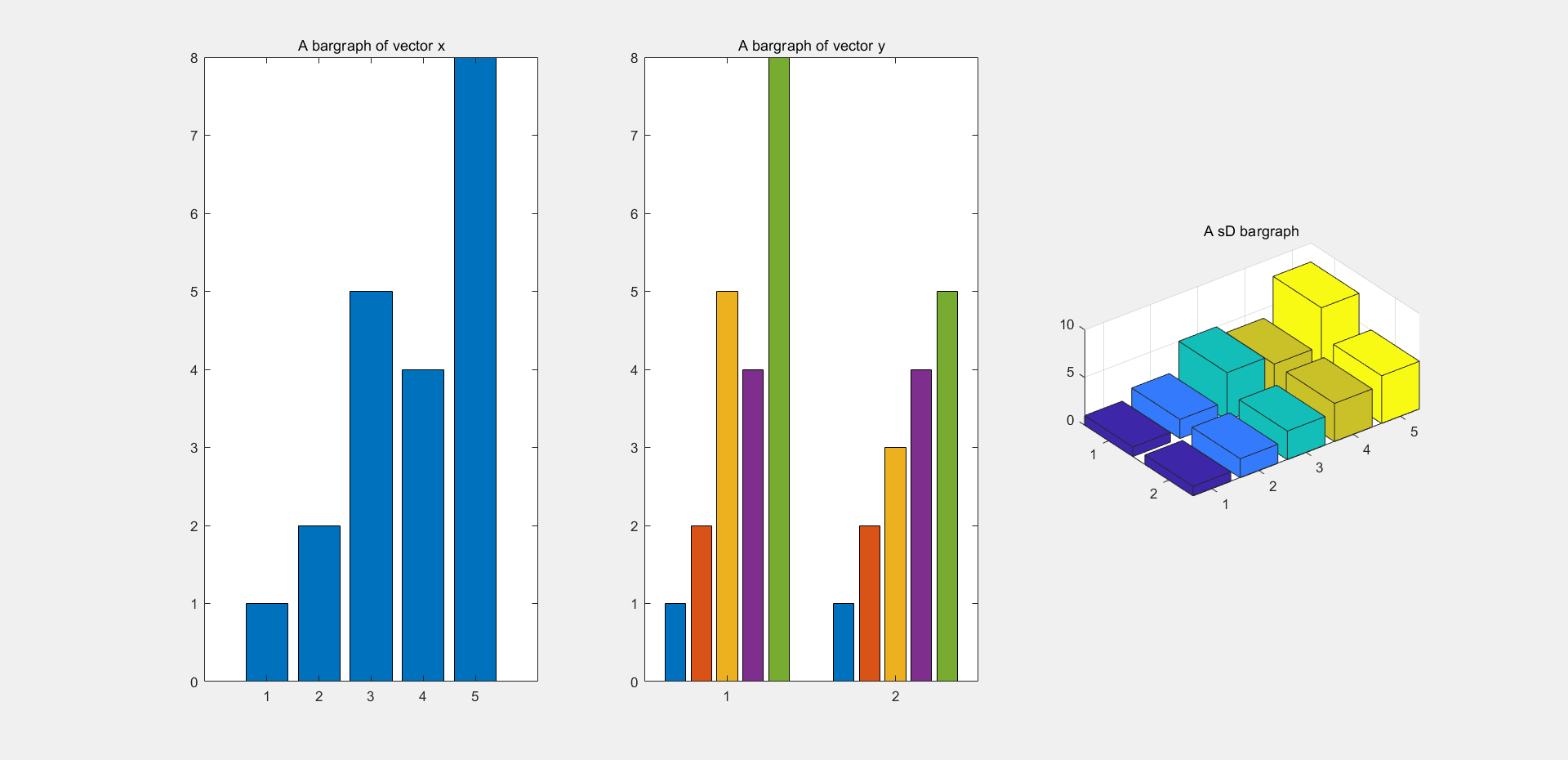
（3）直方3D图的绘制

1
2
3
4
5
6
7
8
9
10
11
12
13
x=[1 2 5 4 8];
y=[x;1:5];
subplot(1,3,1);
bar(x);
title('A bargraph of vector x');

subplot(1,3,2);
bar(y);
title('A bargraph of vector y');

subplot(1,3,3);
bar3(y);
title('A sD bargraph');

绘图结果：

image-20201011185053200

图一绘制了x的直方分布图，其中x是一个一行五列的矩阵（也可称向量）；图二绘制了y的直方分布图，其中y是一个两行五列的矩阵；图三则绘制了y的3D直方图。

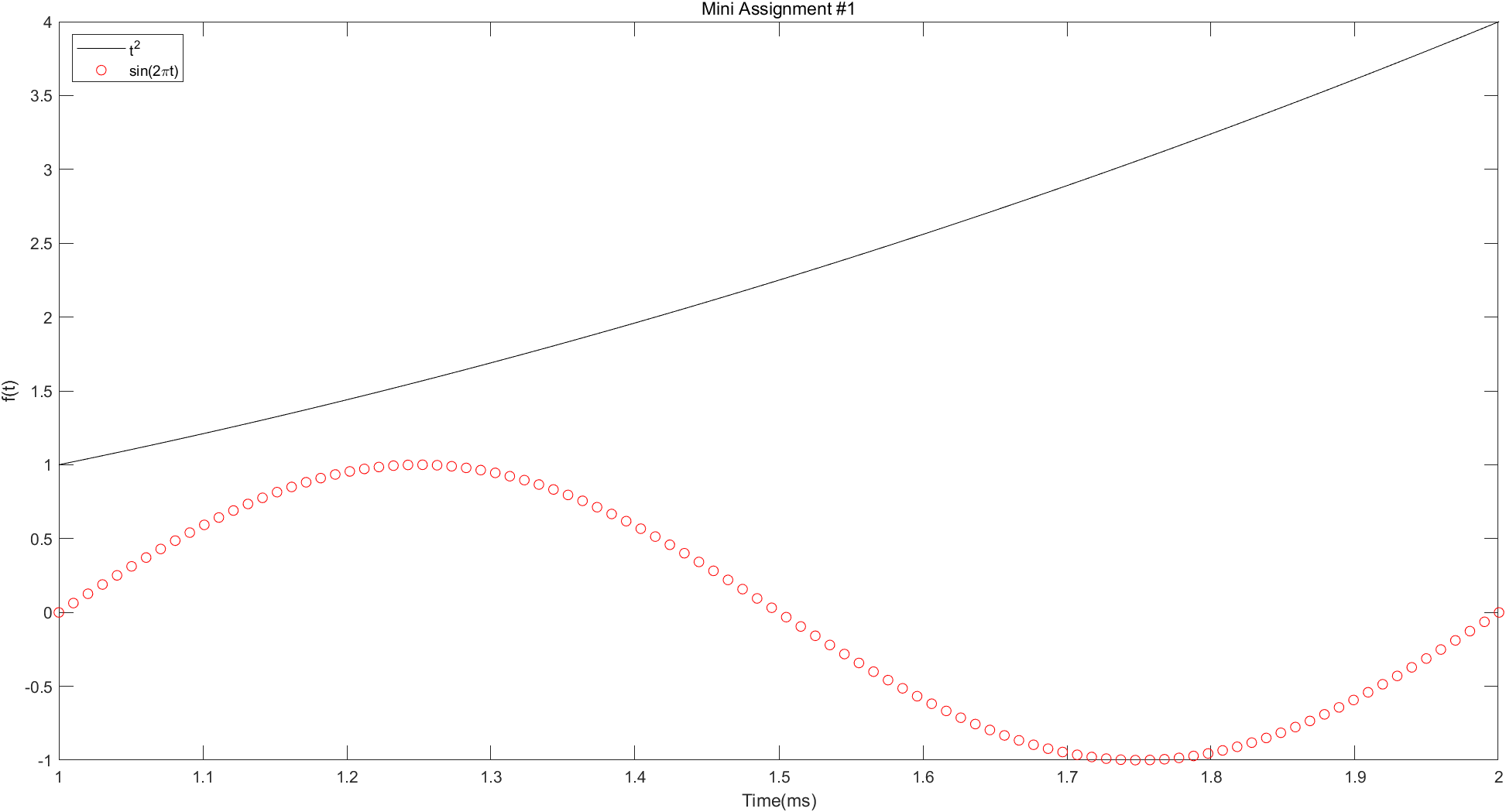
8、练习题目

（1）Exercise One

1
2
3
4
5
6
7
8
t=linspace(1,2);
f=t.*t;
g=sin(2.*pi*t);
plot(t,f,'k-',t,g,'ro');
xlabel('Time(ms)');
ylabel('f(t)');
title('Mini Assignment #1');
legend('t^2','sin(2\pit)','Location','northwest');

绘图结果：

image-20201011192013588

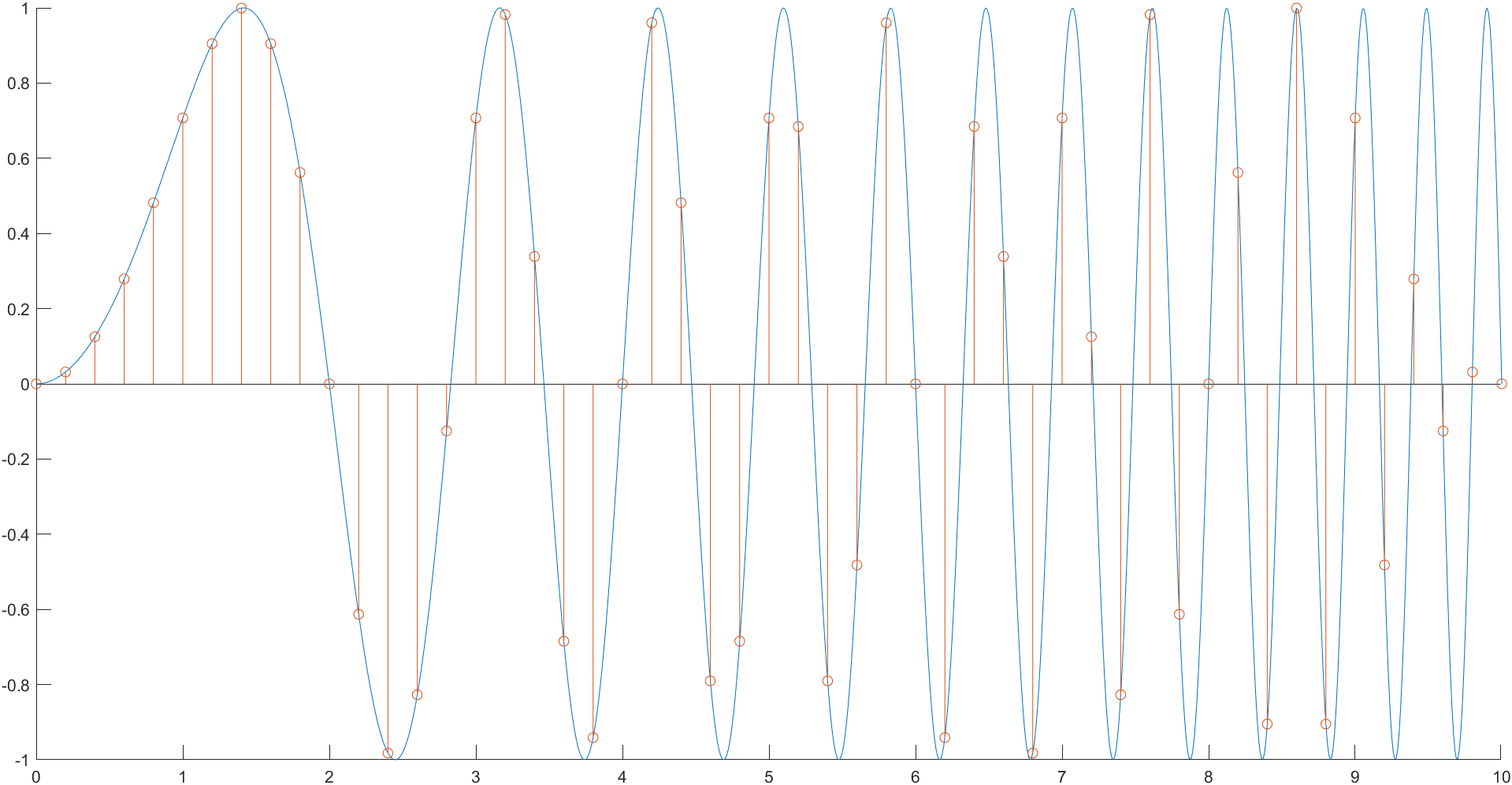
（2）Exercise Two

1
2
3
4
5
6
7
8
9
hold on
t=0:0.01:10;
f=sin(pi.*t.*t/4);
plot(t,f);

x=0:0.2:10;
y=sin(pi.*x.*x/4);
stem(x,y);
hold off

绘图结果：

image-20201011192309727